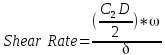Scale-up of Geometrically Similar Extruders

Scale-up of geometrically similar extruders is relatively straight-forward:

This sounds deceptively easy.  It really can be this easy.  The largest caution in scaling up the die is a significant change in geometry for the die between pilot plant and production plant.  More than one manufacturer uses a pilot plant set-up that puts the die opening(s) directly in front of the screw with no obstructions, but a much more restrictive design on a commercial scale.  When a page is added on this subject, a link will be added here. 

Below is a simple description of why geometrically similar extruders scale-up in the manner described above.  More comprehensive and and rigorous descriptions are possible, but will not be covered here. 

Throughput and Heat Transfer in Geometrically Similar Extruders


Extruders designed to be geometrically similar are a case where direct scale-up is possible if some basic assumptions are not violated.  If two extruders are geometrically similar, it means that they look exactly alike except for the size of the extruders.  Every dimension of the extruder is multiplied by some constant.  One way to think of this is with scale models in the same way there are scale models of trains, planes, and cars.  These scale models are models of the real item that have been shrunk in every dimension.  Alternately, if you are somewhat familiar with CAD software, it is similar to zooming in on an object: what shows on the screen has the same relative dimensions, with all dimensions being increased by the same amount. 

The major basic assumptions to be aware of include:

If two extruders are geometrically similar, then we can do some basic analysis of the system to demonstrate how the throughput of the extruder scales up with diameter of the extruder and why extruders should not be actively heated or cooled if there is a desire to scale the process. 

First we need to look at the geometry of the screw in a scale-independent (dimensionless) manner.  The screw element has the following characteristics:

Dimension
 Symbol indicating this variable
 Notes on the variable
Diameter of the screw
 D  This is the basis for 1 unit of length measurement for the extruder.  All other dimension will be converted in terms of D. 

This measurement is also referred to as the outer diameter (Do). 
Inner diameter of the screw
 Di This is the narrowest dimension on the screw, basically the diameter of the screw (D) minus double the depth of the channel  defined by the flights.  This is fixed on typical twin-screw extruders, but may change along the length of the extruder for a single-screw extruder or for twin-screw extruders where the 2 screws are not parallel. 
Flight thickness
 t
 This can be a constant thickness from the root diameter to the outer diameter, but is more typically variable and defined by the elliptical channel. 

Length
 L
 This is the length of the extruder.  Extruder lengths are often expressed in terms of diameters. 
Pitch
 P
 This is the distance forward material in the screw would travel per revolution of the screw in the area of this pitch.  A full pitch screw would move material forward 1 D, 3/4 pitch would move material forward 0.75 D, etc, assuming there are no inefficiencies in the conveying of the screw. 
Gap between the barrel wall and the diameter of the screw part

δ

This is 1/2 the difference in diameter for the barrel and the screw.
Fraction of the barrel cross-sectional area occupied by the screw elemnt
 C1 This is a mathematical constant across scales for geometrically similar extruders
Ratio of the barrel diameter to screw diameter
C2
 The barrel diameter is slightly larger than the screw.  Using a ratio of barrel diameter to screw diameter will make the math more easily understood.
Created Variable
 C3
 A constant that is a combination of a function of C1 and C2.  Use of C3 will make some later calculations be easier to work with. 

Diagram of a screw element (side view):

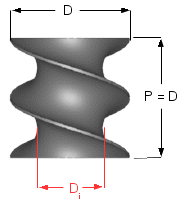
Image of screw should show up here.

Looking at the side view of a screw element, we can see that for 1 full revolution of a screw, the screw will convey the extrudate forward equal to the pitch of the screw.  This ignores any inefficiencies in pumping ability in the screw.  These inefficiencies in pumping will also scale, and that will be covered a bit later in this page.  So: the volume of extrudate conveyed forward is proportional to the diameter of the extruder.

One revolution of a screw brings the extrudate forward by the pitch of the screw (a full pitch screw for this example):

Equation image should show up here

Diagram of a screw element (end view):

Image of screw from the end

The blue in the image above indicates the cross-section of the metal at the end of the screw.  This is the area of the cross-section in the barrel that is not extrudate.  The barrel is a slightly larger diameter than the screw, so if we show a cross-section of the extruder with both the extrudate (red) and the metal of the screw (blue), the full cross-section of the barrel can be visualized:
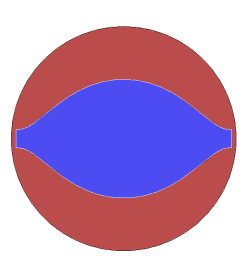
Image of cross-section of the screw and extrudate

If the cross-section of the metal is removed, we are left with just the cross-section of the extrudate:
Image of cross-section of the extrudate

The portion of the cross-sectional area of the barrel contains the screw element, not extrudate.  This can be calculated:

Equation image should show up here

This area is proportional to some set of constants multiplied by D2.  Increasing or decreasing the diameter is exactly as if an image of the extrudate cross-sectional volume is being zoomed in or out: the percentage of the area of the barrel that is extrudate is unchanged by the diameter of the extruder. 

The cross-sectional area of the barrel can be calculated:

Equation image should show here
Now the volume of extrudate being conveyed forward can be calculated:
Equation image should show up here

The constant C3 was created to make the equation show a little more clearly for later calculations. 


So now we have the volume of extrudate carried forward per revolution of the screw by multiplying the cross-sectional area of the extrudate by the length the extruate is conveyed forward:

Equation image should show up here


This tells us that the volume conveyed forward in an extruder screw is proportional to the diameter of the screw cubed. A similar calculation can be done to show the same relationship applies for twin-screw extruders. Since the residence time is proportional to diameter of the extruder for geometrically similar extruders, residence time is independent of extruder diameter for geometrically similar extruders being fed scaled feed rates and at equal screw speeds.


Heat Generation in Extruders:

Heat generation in extruders occur through viscous dissipation of energy being delivered through the extruder screw(s). Energy input is a function of shear rate of the extrudate. It can be shown that for geometrically similar extruders fed at scaled feed rate, the energy input is a function of shear rate and time in the extruder. The shear rates can be calculated for any point in the extrudate. For the sake of an easy geometry, a cross-section of the screw (in blue) and the extrudate (in red) will be used for the example.  This is shown in the image below.  The diameter of the barrel is D+2δ where δ is the gap between the screw element and the barrel wall at the narrowest point.  For different areas in the extrudate, the distance  between the moving screw element and the barrrel wall will be different.

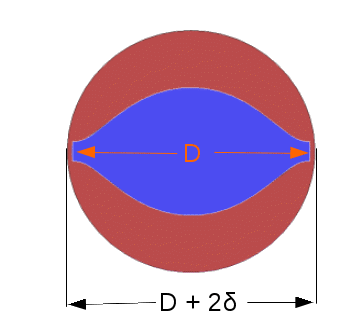
  Image should show up here

For this example, we use the area of highest shear for the calculation, but the shear at any point could be used.  The gap between the screw tip and the wall is the point of highest shear and can be expressed mathematically as:


Equation image should show up here

where C2 is the ratio of barrel diameter to screw diameter (as above), where ω is the rotational speed in radians/second of the extruder, and δ in meters is the gap between the outside edge of the paddle and the wall.  Note that the gap is proportional to the diameter, so that if the diameter is doubled, the gap is also doubled.  This means that the shear rate is independent of screw diameter for geometrically similar extruders.  This calculation can be repeated for any point in the extrudate flow with the shear rate on any two scales being equal for any given dimensionless position in the extrudate.  Shear rates are matched in two different diameters of geometrically similar extruders being operated at scaled feed rates and equal screw speeds.  Since residence time and shear rates are both matched, energy input per unit mass (SME) to the extrudate on both scales is equal.

Heat Exchange in Extruders:

The math here is a bit easier: the surface area to remove heat from an extruder is the area of the barrel wall.  If we consider a length of the extruder that is 1D in length we can show the area for heat exchange is proportional to D2.

Equation image should show up here

This means that as the diameter of the extruder is increased, the temperature difference between the extrudate and cooling (or heating) medium must be proportional to 1/D.  There are at least two ways to handle this.  The first is to have the jacket medium deliver a temperature difference relative to 1/D.  This gets to be difficult for large diameter extruders.  The second approach is to use no heating or cooling on the barrel, minimizing any heat transfer through the barrel wall.  This second approach will tend to be more scalable, if the characteristics of the desired product can be delivered without heating or cooling of the barrel. 

For geometrically similar extruder being fed at scaled rates and run at a given RPM, the feed rate increases at a rate proportional do D3.  Since energy input per unit mass is constant and the mass flow rate is proportional to D3,  the energy input to the extruder is a function of D3.  The area available for heat exchange is only proportional to  D2: surface area available per unit mass is proportional to 1/D.

Equation image should show up here

Geometrically Similar Extruder Elements in Extruders with Different Lengths

Sometimes there are situations where extruders with geometrically similar screw elements in extruders with different lengths.  In some cases, this can be accommodated without significant impacts to the process. 

The easier example is when scaling from a shorter extruder to a longer one.  In this case, the shorter extruder can be scaled to the longer one by adding conveying elements in the early part of the extruder screw profile.  The added conveying elements would not be filled, so would add minimal extra energy to the extrudate.  The one area to be a little cautious may be in the location of the first set of paddles (kneading blocks).  In many cases, the first set of paddles are used as a way to seal the screws and prevent injected steam from exiting through the extruder inlet.  In cases like that, the conveying screws should be added after the first set of paddles, again it should have minimal impact on the energy input to the extrudate.

The more difficult situation is going from a longer extruder to a shorter one.  In a screw profile with a lot of paddles or other work elements, it may not be possible to remove conveying elements due to there not being enough remaining conveying elements force all the extrudate to be conveyed through the die - the extruder will back up.